Volume Of A Sphere Differential Equation

Triple integrals can often be more readily evaluated by using cylindrical coordinates instead of rectangular coordinates. Some common equations of surfaces in rectangular coordinates along with corresponding equations in cylindrical coordinates are listed in . These equations will become handy as we proceed with solving problems using triple integrals. Consider the region inside the right circular cylinder with equation bounded below by the -plane and bounded above by the sphere with radius centered at the origin (). Set up a triple integral over this region with a function in cylindrical coordinates.

A similar situation occurs with triple integrals, but here we need to distinguish between cylindrical symmetry and spherical symmetry. In this section we convert triple integrals in rectangular coordinates into a triple integral in either cylindrical or spherical coordinates. Express the volume of the solid inside the sphere and outside the cylinder that is located in the first octant as triple integrals in cylindrical coordinates and spherical coordinates, respectively. Express the volume of the solid inside the sphere and outside the cylinder as triple integrals in cylindrical coordinates and spherical coordinates, respectively.

Also recall the chapter opener, which showed the opera house l'Hemisphèric in Valencia, Spain. It has four sections with one of the sections being a theater in a five-story-high sphere under an oval roof as long as a football field. Inside is an IMAX screen that changes the sphere into a planetarium with a sky full of twinkling stars. Using triple integrals in spherical coordinates, we can find the volumes of different geometric shapes like these.

A sphere is defined as a set of points in three-dimensional space, that are all at the same distance from a given point, which is called the center. Sphere is widely used in physics to model different objects, like spherical capacitors or atoms of a gas. You should also check out our spherical coordinates calculator and see how you can use a sphere to describe the position of any given point in a 3D space. We have reached the expression, eq , for the volume of an approximate sphere from a description in terms of the usual polar coordinates, r, θ, ϕ.

Unfortunately the radius and its derivative with respect to the central angle are not directly measurable. To make the analysis correspond more closely to the measured quantities, we will look at a description of an object as the "envelope" of a set of tangent planes. The analytical description was developed by Meissner in a study of objects of constant breadth.

Equivalent graphical methods are used in the design of gears and cams, for example . More recent work has been published by Goldberg . We first want to find the volume of the balloon.

If we look at the top part and the bottom part of the balloon separately, we see that they are geometric solids with known volume formulas. However, it is still worthwhile to set up and evaluate the integrals we would need to find the volume. If we calculate the volume using integration, we can use the known volume formulas to check our answers.

This will help ensure that we have the integrals set up correctly for the later, more complicated stages of the project. In this project we use triple integrals to learn more about hot air balloons. The top of the balloon is modeled by a half sphere of radius feet.

The bottom of the balloon is modeled by a frustum of a cone . The radius of the large end of the frustum is feet and the radius of the small end of the frustum is feet. A graph of our balloon model and a cross-sectional diagram showing the dimensions are shown in the following figure. As stated before, spherical coordinate systems work well for solids that are symmetric around a point, such as spheres and cones. Let us look at some examples before we consider triple integrals in spherical coordinates on general spherical regions.

In three-dimensional space in the spherical coordinate system, we specify a point by its distance from the origin, the polar angle from the positive , and the angle from the positive and the line (). Note that and (Refer to Cylindrical and Spherical Coordinates for a review.) Spherical coordinates are useful for triple integrals over regions that are symmetric with respect to the origin. Consider the region inside the right circular cylinder with equation bounded below by the -plane and bounded above by Set up a triple integral with a function in cylindrical coordinates. The concept of triple integration in spherical coordinates can be extended to integration over a general solid, using the projections onto the coordinate planes. Note that and mean the increments in volume and area, respectively. The variables and are used as the variables for integration to express the integrals.

Cylindrical coordinate systems work well for solids that are symmetric around an axis, such as cylinders and cones. Let us look at some examples before we define the triple integral in cylindrical coordinates on general cylindrical regions. We can use triple integrals and spherical coordinates to solve for the volume of a solid sphere. Circular cylinderCircular coneSphereParaboloidRectangularCylindricalAs before, we start with the simplest bounded region in to describe in cylindrical coordinates, in the form of a cylindrical box, ().

Suppose we divide each interval into subdivisions such that and Then we can state the following definition for a triple integral in cylindrical coordinates. In three-dimensional space a point with rectangular coordinates can be identified with cylindrical coordinates and vice versa. We can use these same conversion relationships, adding as the vertical distance to the point from the -plane as shown in the following figure. Suppose the volume of a sphere of radius r unit is changing at a rate proportional to its surface area. Write a differential equation for the volume of the sphere.

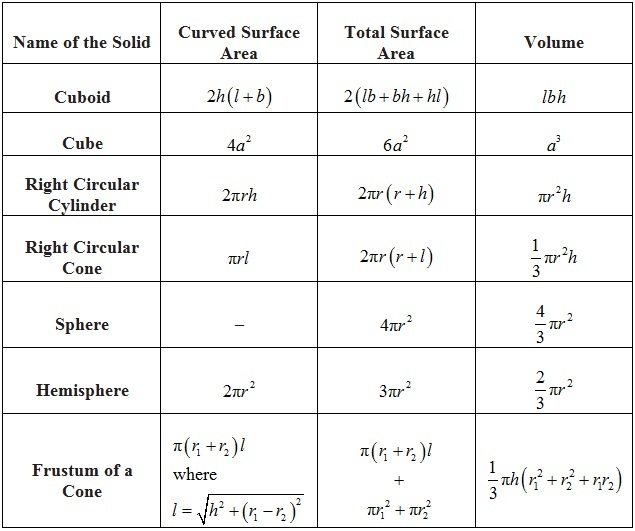
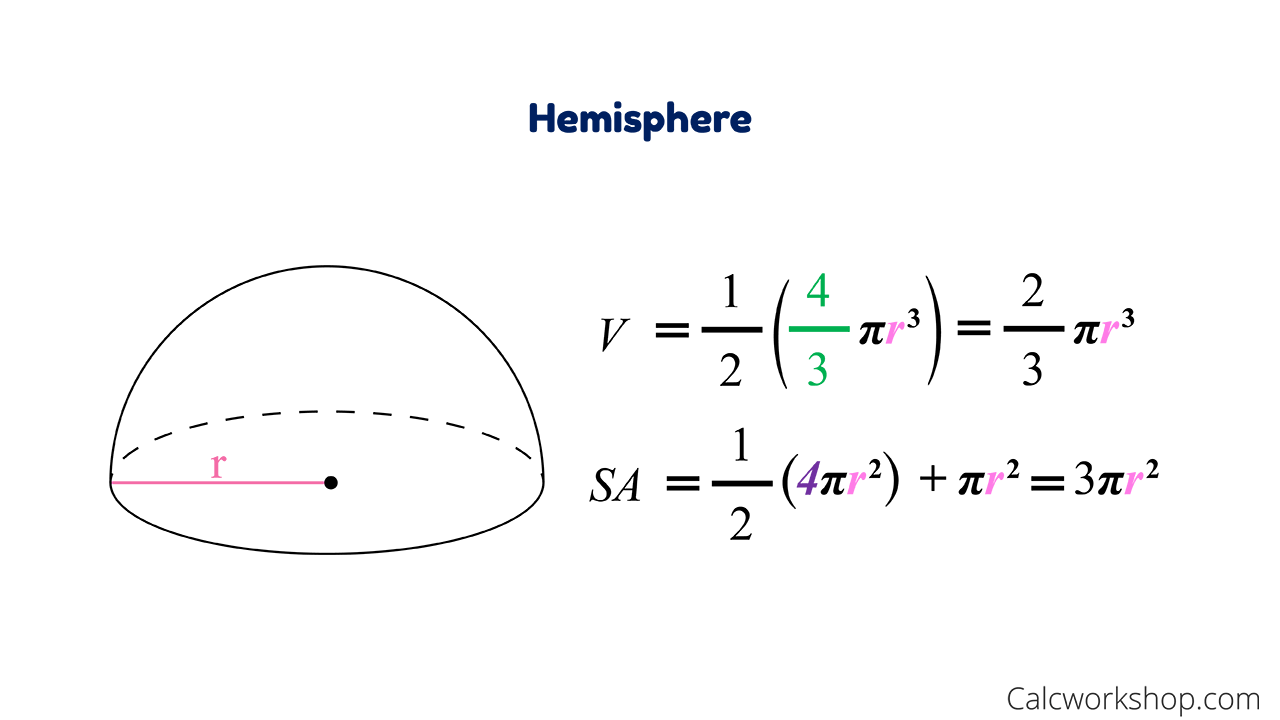
Use V App and S 4xtra for the volume and surface area of a sphere of radius r, respectively. Use spherical coordinates to find the volume of the triple integral, where ??? The unit of volume of a sphere is given as the 3. The metric units of volume are cubic meters or cubic centimeters while the USCS units of volume are, cubic inches or cubic feet. The volume of sphere depends on the radius of the sphere, hence changing it changes the volume of the sphere.

There are two types of spheres, solid sphere, and hollow sphere. The volume of both types of spheres is different. We will learn in the following sections about their volumes. Rather the measurements yield the breadth, which is the sum of two tangential radii.

Therefore it is important to consider the important class of objects which exhibit odd lobing, with a valley opposite a hill. The local radius near the hilltops is systematically less than the mean radius. We have assumed that they are approximately equal so that the difference leads to errors of a higher order than the second. We can expect the gradient ▽p to approximate ▽r, but at this time have no good basis for estimating its magnitude. In order for the terms of the first order to vanish, it is necessary to have a good average value of p experimentally as well as mathematically.

With the polar coordinate system, when we say , we mean a circle of radius units and when we mean an infinite ray making an angle with the positive -axis. The volume of sphere is the capacity it has. The volume of sphere is measured in cubic units, such as m3, cm3, in3, etc.

The shape of the sphere is round and three-dimensional. It has three axes as x-axis, y-axis and z-axis which defines its shape. All the things like football and basketball are examples of the sphere which have volume. Try deriving for yourself the volume of a sphere by integration. You can start with a surface of a sphere with zero radius, and integrate that out to the radius of your sphere. Think of that as having a a series of infinitesimally thin concentric shells from the center of the sphere out to the full radius of the sphere.

That operation will "sweep" through all the volume of the sphere, accumulating the total volume of the sphere. That being an integration of the surface area through a radius, it's not a coincidence that a derivative of the volume of a sphere with respect to its radius is equal to the surface area. Use a CAS to graph the solid whose volume is given by the iterated integral in spherical coordinates as Find the volume of the solid. Use a CAS to graph the solid whose volume is given by the iterated integral in spherical coordinates Find the volume of the solid. Use a CAS to graph the solid whose volume is given by the iterated integral in cylindrical coordinates Find the volume of the solid Round your answer to four decimal places.

Use a computer algebra system to graph the solid whose volume is given by the iterated integral in cylindrical coordinates Find the volume of the solid. Use the conversion formulas to write the equations of the sphere and cone in spherical coordinates. As we have seen earlier, in two-dimensional space a point with rectangular coordinates can be identified with in polar coordinates and vice versa, where and are the relationships between the variables. A sphere is defined as the set of all points in three-dimensional Euclidean space that are located at a distance (the "radius") from a given point (the "center"). Twice the radius is called the diameter, and pairs of points on the sphere on opposite sides of a diameterare called antipodes. The angle between two spheres at a real point of intersection is the dihedral angle determined by the tangent planes to the spheres at that point.

Two spheres intersect at the same angle at all points of their circle of intersection. They intersect at right angles if and only if the square of the distance between their centers is equal to the sum of the squares of their radii. After rectangular coordinates, the two most common an useful coordinate systems in 3 dimensions are cylindrical coordinates and spherical coordinates . The volume of a 3-dimensional solid is the amount of space it occupies.

Be sure that all of the measurements are in the same unit before computing the volume. Expressions are derived for the volume of an approximate sphere in terms of measured breadth, the distance between parallel planes tangent to opposite sides. Thus, a ball commercially available at moderate cost can be used for absolute density measurements of high accuracy. Similar expressions are given for the area of an approximate circle. In order to find limits of integration for the triple integral, we'll say that ??? Then we only have to find an interval for ???

As a result, geometers call the surface of the usual sphere the 3-sphere, while topologists refer to it as the 2-sphere and denote it . All points of a sphere are umbilics.At any point on a surface a normal direction is at right angles to the surface because the sphere these are the lines radiating out from the center of the sphere. The intersection of a plane that contains the normal with the surface will form a curve that is called a normal section, and the curvature of this curve is the normal curvature. For most points on most surfaces, different sections will have different curvatures; the maximum and minimum values of these are called the principal curvatures.

Any closed surface will have at least four points called umbilical points. At an umbilic all the sectional curvatures are equal; in particular the principal curvatures are equal. Umbilical points can be thought of as the points where the surface is closely approximated by a sphere.For the sphere the curvatures of all normal sections are equal, so every point is an umbilic. The sphere and plane are the only surfaces with this property.

Assume that the volume of the sphere is made up of numerous thin circular disks which are arranged one over the other as shown in the figure given above. The circular disks have continuously varying diameters which are placed with the centres collinearly. A thin disk has radius "r" and the thickness "dy" which is located at a distance of y from the x-axis. Thus, the volume can be written as the product of the area of the circle and its thickness dy. One interesting thing that you should notice is that the surface area to volume ratio is inversely proportional to the size of an object.

For example, we found that for a sphere S/V is 3/R. Since R tells us the "size" we see that S/V is inversely proportional to this (in other words, as R gets small the S/V ratio gets big). We have evaluated the topography correction for the difference between the volume of an approximate sphere and that of a true sphere of the same average breadth. It is of second order in the variations in tangential radius, and therefore much smaller than the random and systematic errors of the measurements which can be made on the object. For example, a commercially available ball bearing of moderate cost can be expected to have a topography correction of a few parts in 109.

Its mean breadth can be measured to a part in 106 corresponding to a few parts in a million in its volume. The cone is of radius 1 where it meets the paraboloid. The projection of the region onto the -plane is the circle of radius centered at the origin. Evaluate a triple integral by changing to spherical coordinates. Evaluate a triple integral by changing to cylindrical coordinates. If the problem had asked for the rate of change of volume as a function of the rate of change of radius, then you would need the derivative.

Here, it is just the algebraic procedure of replacing r with its expression as a function of t. Although the radical plane is a real plane, the circle may be imaginary or consist of a single point . Therefore, we can conclude that the rate of change of total surface area of the sphere is equal to 3 sq cm per second. The volume of a sphere is increasing at the rate of 3 cubic centimetre per second. Find the rate of increasing of its surface area, when the radius is 2 cm. As you can see, the volume equals 4/3 times pi times the radius of a sphere cubed.

Observations with the radial profilometer are essential in estimating the error due to topography. The profiles show the odd as well as the even harmonics. If a single harmonic dominates the topography the number n of lobes can be counted.

If the pattern is irregular, a radial profile provides a sample from which to estimate a mean square rate of change of radius (σq2 in eq ). The angular resolution of the trace is of the order of a degree, so that the chance of finding a small defect is improved. As with the other multiple integrals we have examined, all the properties work similarly for a triple integral in the spherical coordinate system, and so do the iterated integrals. The volume element of a box in spherical coordinates.

The following figure shows a few solid regions that are convenient to express in spherical coordinates. Recall the relationships that connect rectangular coordinates with spherical coordinates. To convert from rectangular to cylindrical coordinates, we use the conversion and To convert from cylindrical to rectangular coordinates, we use and The -coordinate remains the same in both cases.